After my first post on Elliott Waves the visitor count on this blog sky rocketed. It went from less than 1 a day on average to 3 or 4 a day – thats great. This is part one of a planned series about finding Elliott waves in financial data.
Recap of the Algorithm
In my first post about Elliott Waves algorithm in Python I described my idea on how such an algorithm can work: try a lot of combinations of possible 12345 waves (in length (=value) and time). Then, rule out these combinations that do not obey all the rules according to Elliott Wave theory. E.g. wave 3 must not be the shortest wave or wave 4 does not overlapp with wave 1 for an impulse etc.
It turned out, the more rules I implemented, naturally less combinations were found (good). In Elliott Wave Theory, there are rules, which have to be fullfilled 100% of the time and guidelines, which could be fullfilled. For a first step, I only work with the rules given here on page 4 and here.
Algorithm at Work
For sake of simplicity, we consider an upwards trend. Data used ist BTC/USD with daily candles.
Finding Wave 1
The smallest element (we call it MonoWave) in such a trend is that the chart builds consecutive higher highs. Once a candle fails to build a new high, this micro trend is broken and a MonoWaveUp is formed. The MonoWaveUp starts from the low of the first candle (low, index_low [a DateTime object)) and ends at the high of this candle (high, index_high).
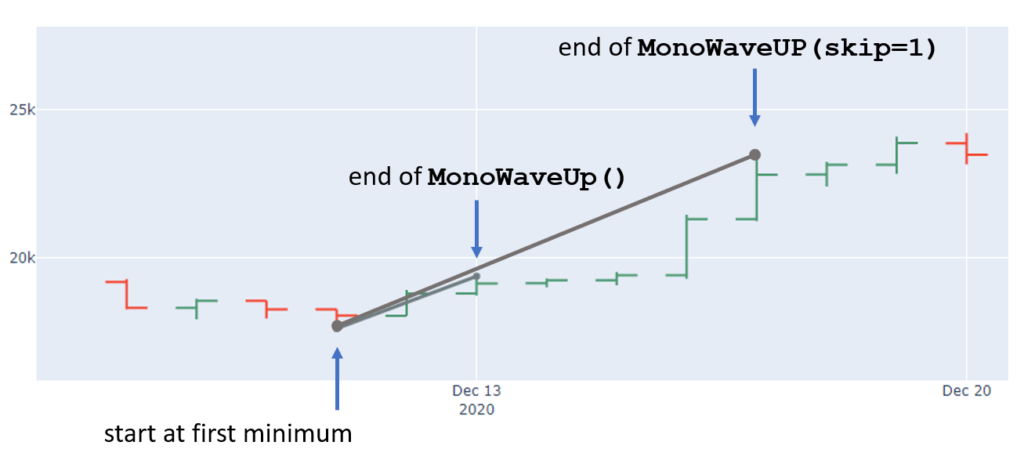
The MonoWaveUp (inherited from an ABC MonoWave) has properties like .length (in value) and .duration (number of candles; time-wise).
Via the parameter skip, we will find longer waves by skipping intermediate max- / minma.
Finding Wave 2
From this local high, the same algorithm is now going down the trend looking for lower lows to find the end of wave 2 The wave 2 is then a MonoWaveDown instance.
From here we go and find the next MonoWaveUp building wave 3, following a MonoWaveDown (wave 4) and finally a MonoWaveUp builds wave 5.
In case no wave is found, e.g. the data ends or the chart is only going down while trying to find a wave up the function will return None.
Building a WavePattern
Once 5 waves are found, they build a WavePattern object which we can plot and on which we check the wave rules .
A (5 fold) WavePattern is described by a tuple of integers, denoting how many intermediate maxima / minima are skipped, e.g. [0, 0, 0, 0, 0] means: finding all consecutive max- / minima witout skipping intermediate extrema.
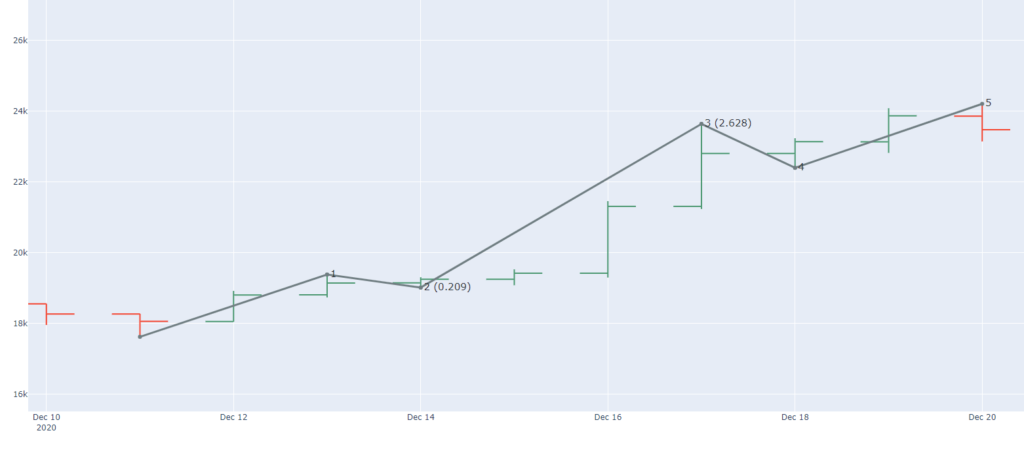
Numbers in brackets denote the correction meassured by the previous wave (needed to look for Fibonacci levels).
[5, 0, 0, 0, 0] means, that for the MonoWaveUp, the first occuring maxima is ignored. This list is called a WaveConfig.
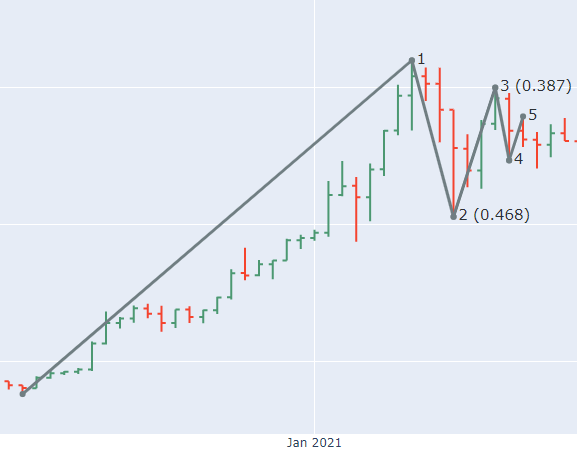
Applying a WaveRule to a WavePattern
We go through a lot of combinations o(10M+). For each WavePattern, we apply the WaveRule, e.g. for an impulse, and check if it is valid. A WaveRule is inherited from the abstract base class WaveRule. The user has to implement the .set_conditions() function, which returns True if all rules are fullfilled.
The rules are encoded in a nested dictionary, with a rule name, e.g. w2_1 as key and a dict with the waves needed for this rule, a function and a message which should be printed in case of rule violation.
conditions = { # WAVE 2
"w2_1": {
"waves": ["wave1", "wave2"],
"function": lambda wave1, wave2: wave2.low > wave1.low,
"message": "End of Wave2 is lower than Start of Wave1.",
},
"w2_2": {
"waves": ["wave1", "wave2"],
"function": lambda wave1, wave2: wave2.length >= 0.2 * wave1.length,
"message": "Wave2 is shorten than 20% of Wave1.",
},
"w2_3": {
"waves": ["wave1", "wave2"],
"function": lambda wave1, wave2: 9 * wave2.duration > wave1.duration,
"message": "Wave2 is longer than 9x Wave1",
},
# WAVE 3
"w3_1": {
"waves": ["wave1", "wave3", "wave5"],
"function": lambda wave1, wave3, wave5: not (
wave3.length < wave5.length and wave3.length < wave1.length
),
"message": "Wave3 is the shortest Wave.",
},
"w3_2": {
"waves": ["wave1", "wave3"],
"function": lambda wave1, wave3: wave3.high > wave1.high,
"message": "End of Wave3 is lower than End of Wave1",
},
"w3_3": {
"waves": ["wave1", "wave3"],
"function": lambda wave1, wave3: wave3.length >= wave1.length / 3.0,
"message": "Wave3 is shorter than 1/3 of Wave1",
},
"w3_4": {
"waves": ["wave2", "wave3"],
"function": lambda wave2, wave3: wave3.length > wave2.length,
"message": "Wave3 shorter than Wave2",
},
"w3_5": {
"waves": ["wave1", "wave3"],
"function": lambda wave1, wave3: 7 * wave3.duration > wave1.duration,
"message": "Wave3 more than 7 times longer than Wave1.",
},
# WAVE 4
"w4_1": {
"waves": ["wave1", "wave4"],
"function": lambda wave1, wave4: wave4.low > wave1.high,
"message": "End of Wave4 is lower than End of Wave1",
},
"w4_2": {
"waves": ["wave2", "wave4"],
"function": lambda wave2, wave4: wave4.length > wave2.length / 3.0,
"message": "Length of Wave4 is shorter than 1/3 of End of Wave1",
},
# WAVE 5
"w5_1": {
"waves": ["wave3", "wave5"],
"function": lambda wave3, wave5: wave3.high < wave5.high,
"message": "End of Wave5 is lower than End of Wave3",
},
"w5_2": {
"waves": ["wave1", "wave5"],
"function": lambda wave1, wave5: wave5.length < 2.0 * wave1.length,
"message": "Wave5 is longer (value wise) than Wave1",
},
}
Only if all rules are fullfilled, the WavePattern is valid.
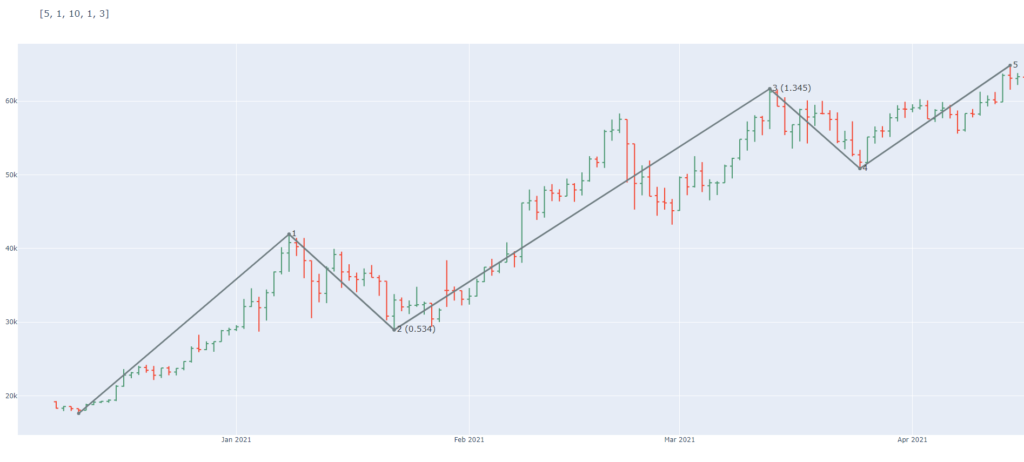
You can now start and try various combinations or run a script and loop over pre-calculated WaveOptions. As an example, we can easily find this Elliott Wave count for the Bitcoin chart. The corresponding WaveOptions are in the upper left: [5,1,10,1,3]. First 5 maxima are skipped, then the next minimi is skipped and so on.
Problems with the implementation
At the moment the package is able to find impulsive (12345) movements followed by a valid ABC correction in a given OHLC data set. As you may know form the wave gurus, there is always a second count around the corner. This count can be pulled out in case their market forecast was wrong the initial count turns invalid.
Indeed, looking at a chart, there are plenty of counts possible. All counts (on all times cales) mix into each other and for the eye its diffucult to validate (all) the Elliott Wave rules, e.g. given by Prechter et al.
Iterative Search
The algorithm is planned to work from the smallest (small in time and value) possible counts upwards in wave degree. A 12345 – ABC cycle, which is the shortest (time and value) turns into a I-II setup on the next time scale.
However, for each 12345 there are multiple ABC corrections possible, from which multiple 12345 trend continuations are possible. One has to build a fractal structure of the chart and later look from large to small timeframes, as all wave counts on all time scales have to be valid (checked against the rules).
I intend to trade wave 3 setups (also called Tiedje Dream Wave), but to have a valid setup, you have to have a valid impulsive movement for a I count (i.e. a 12345 as an impulse) and an ABC correction (zig zag) forming the II. So at least two wave degrees are consinderd.
One can go up and down in time frames and should / could always find waves (fractal market structure). I need to implement an iterative search for finding wave patterns. This is the part where I work at the moment. Please feel free to drop a mail / contribute on github if you have good ideas for doing so.
I also think about giving each wave count something like a score. Depending on the number of guidlines and/or rules which are fullfilled, we can then rank the counts.
Outlook
From here, we can apply basically the same search algorithm (but downwards) from the end of wave 5 to look for an ABC correction (zig zag). As the standard correction is threefold, the WaveOptionsGenerator only yields tuples of 3, i.e [i,j,k,None,None] for finding the correction. The WavePattern for a correction is then the sequence of [MonoWaveDown, MonoWaveUp, MonoWaveDown].
https://github.com/btcorgtfo/ElliotWaveAnalyzer you have linked is not available..
Hello Steven,
An FYI: your Github link is broken.
fixed
can i have your code…becoz i dont hoe to find patter for historical data
repo is public now
Thank you so much for your suggest in coding elliot wave. God bless you.
Wow thats really awesome.